Tuesday, April 30, 2024
Home » Linear Regression
Machine Learning

Linear Regression

by IndiaSuccessStories
written by IndiaSuccessStories 0 comment

Linear Regression

Introduction

Linear regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables. It assumes a linear relationship between the independent variables and the dependent variable.

In simple linear regression, we model the relationship between one independent variable x and one dependent variable y as a straight line:

y=β0​+β1​x+ε

where:

  • y is the dependent variable,
  • x is the independent variable,
  • β0​ is the intercept,
  • β1​ is the slope,
  • ε is the error term.

Here's a simple example to illustrate linear regression:

Let's consider a scenario where we predict the salary of an employee based on their years of experience. This is a classic example often used to illustrate simple linear regression.

 

1. Collect Data

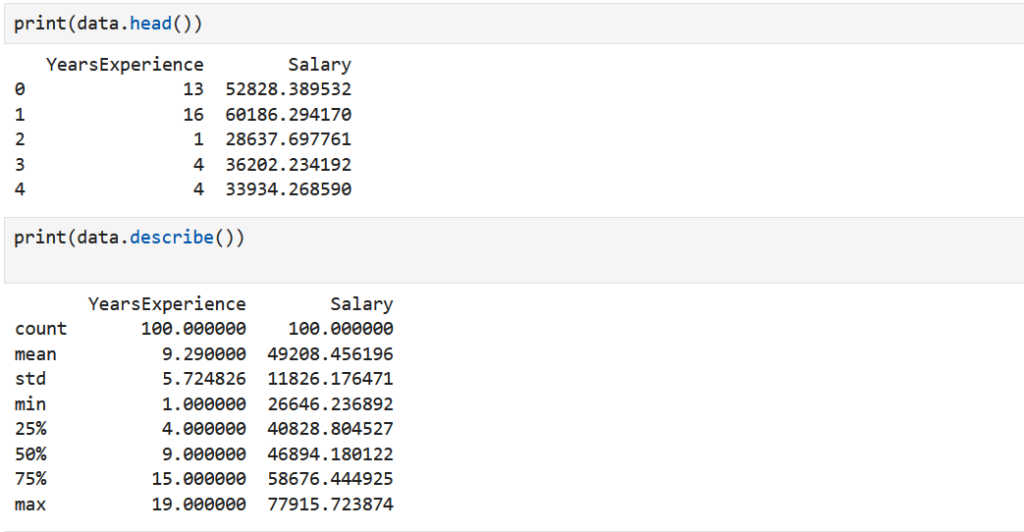
Suppose we have collected data on the years of experience and the corresponding salary of employees. For this example, let's create a synthetic dataset:

  • We generate synthetic data for years of experience and salary.
  • Years of experience range from 1 to 20 years.
  • Salary is generated using a linear equation with some noise.

2. Explore the Data

We print the first few rows and summary statistics of the dataset to understand its structure and distribution.

3. Prepare Data

We separate the independent variable (years of experience) and the dependent variable (salary):

4. Split Data

We split the data into training and testing sets:

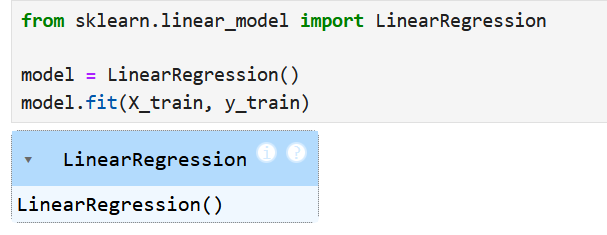
5. Create and Fit Model

We create a linear regression model and fit it to the training data:

6. Make Predictions

We use the fitted model to make predictions on the test data:

7. Evaluate Model

We evaluate the model's performance using metrics such as mean squared error (MSE) and R-squared:

8. Visualize Result

We visualize the relationship between years of experience and salary, along with the regression line:

You Might Also Like

Indian Success Stories is committed to inspiring the world’s visionary leaders who are driven to make a difference with their ground-breaking concepts, ventures, and viewpoints. Join together with us to match your business with a community that is unstoppable and working to improve everyone’s future.

You may also like

Types of clustering algorithms

K Means Clustering

Hierarchical clustering

Clustering

Apriori

Random Forest Classification

Leave a Comment

Save my name, email, and website in this browser for the next time I comment.

Indian Success Stories Logo

Indian Success Stories is committed to inspiring the world’s visionary leaders who are driven to make a difference with their ground-breaking concepts, ventures, and viewpoints. Join together with us to match your business with a community that is unstoppable and working to improve everyone’s future.

Facebook Twitter Youtube Linkedin Envelope Rss

Useful Links

Edtior's Picks

Types of clustering algorithms
K Means Clustering
Hierarchical clustering

Latest Articles

Types of clustering algorithms
K Means Clustering
Hierarchical clustering
Clustering

Copyright © 2024 Indian Success Stories. All rights reserved. 

@2021 - All Right Reserved. Designed and Developed by PenciDesign