CS202: Discrete Structures Certification Exam Answers

CS202: Discrete Structures Exam Quiz Answers

Question 1: Which of the following set pairs are equal sets? Select one:

• X = {1, 3, 9, 7}; Y = {3, 1, 7}
• X = {1, 3, 9, 7}; Y = {3, 1, 5, 9}
• X = {1, 3, 9, 7}; Y = {3, 1, 7, 9}
• X = {1, 3, 9, 7}; Y = {1, 3, 9, 7, 11}

Question 2: Consider the sets X and Y in this figure. What type of set is Y?

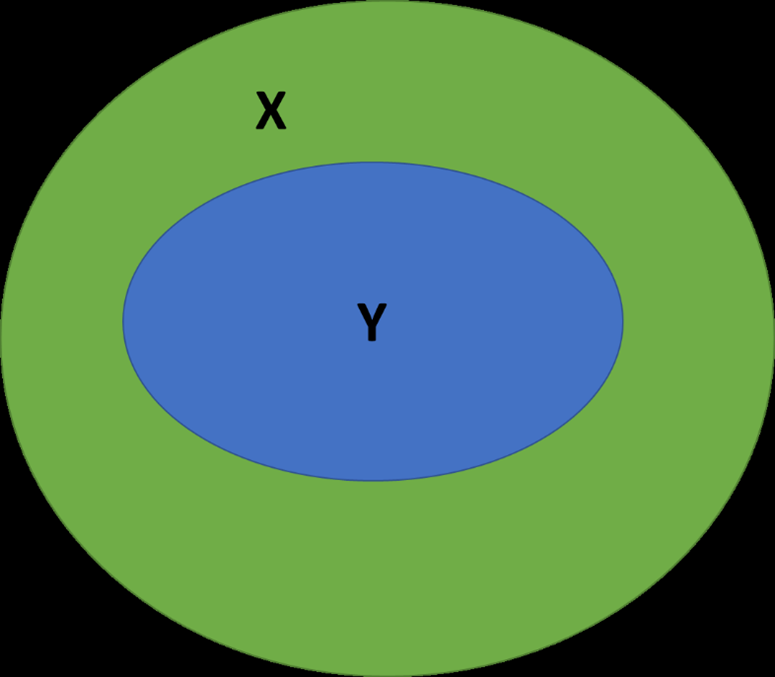
Select one:

• Y is equal to X
• Y is a subset of X
• Y is a superset of X
• Y is equal to the null set

Question 3: Assume there are three sets: W, X, Y. What equation results in the intersection of those sets? Select one:

• W – X – Y = Z
• W ∪ X ∪ Y = Z
• W ⋂ X ⋂ Y = Z
• W ⊕ X ⊕ Y = Z

Question 4: Which of the following is (A − B) ∪ (A ∩ B) ∪ (B − A) equal to? Select one:

• A
• B
• A ∪ B
• The empty set

Question 5: Which of the following is the underlying assumption that is necessary for the Rule of Products to hold true? Select one:

• Elements in set X depend on specific elements in set Y
• Elements in set X must be independent of elements in set Y
• Elements in set X must entirely overlap with elements in set Y
• Elements in set X must be completely different from elements in set Y

Question 6: How many subsets does the set a, b, c�, �, � have? Select one:

• 6
• 7
• 8
• 9

Question 7: We would define the term “proposition” as a sentence that has which of the following qualities? Select one:

• It can only meaningfully be called “completely true”
• It can meaningfully be either “completely true” or “completely false”
• It is “partially true”, where “partially” refers to some degree of truth
• It is “partially false”, where “partially” refers to some degree of falsehood

Question 8: Consider the equation p → (p ∨ q). What is the result if both p and q are false? Select one:

• True
• False
• Cannot be determined
• This is not a logical proposition

Question 9: 3c.1. Assume that a system has three events (E1, E2, E3) that must take place before a fourth event, E4, can occur. Which of the following logical equations ensures the first three events take place before the fourth event? Select one:

• E4 = E1 ^ E2 ^ E3
• E4 = E1 v E2 v E3
• E4 ⇔ E1 ⇔ E2 ⇔ E3
• E4 = ᆨE1 ^ ᆨE2 ^ ᆨE3

Question 10: You have the following requirement: The computer’s run light (L) should come on when power (P) has been applied and the computer is ready to function (F), and when the computer’s start button (S) is pressed or data (D) begins to flow to the computer’s functioning input port (I). Which of the following logical equations would fulfill this requirement? Select one:

• L = (P ^ F) ^ (S ^ (D ^ I))
• L = (P ^ F) ^ (S ∨ (D ^ I))
• L = (P ∨ F) ∨ (S ^ (D ∨ I))
• L = (P ∨ F) ∨ (S ∨ (D ∨ I))

Question 11: If Mary helps Michael so that he gains new abilities that enable his task’s completion, and Michael uses his new abilities to help Susan so that Susan is successful, what role does Mary play in Susan’s success? Select one:

• Mary has been enabled by Susan
• Mary has been enabled by Michael
• Mary has an implied role in Susan’s success
• Mary has nothing to do with Susan’s success

Question 12: In an inductive proof of, ∀n P(n), n = 0, 1, 2, 3, …, …, …, n, …, which of the following is the base case? Select one:

• Showing P (0)
• Showing P(n)
• Proving P(n-1) ⟹ P(n), n = 1, 2, 3, ….
• Proving P(n) ⟹ P (n + 1), n ∈ ℕ, the natural numbers

Question 13: A new deck of playing cards has 52 cards. What is the probability that an ace is drawn on the second trial if a face card is drawn on the first trial and not placed back into the deck? Select one:

• 3/13
• 4/51
• 4/51
• 11/52

Question 14: On a 10-question true-or-false test, if you answer by flipping a coin, which of the following is P (getting a grade of 100%) the same as? Select one:

• 0
• 1/ (210)
• 1/10
• ½

Question 15: Consider a collection of independent events, each of which produces one of the following temperatures in a boiler {22, 23, 22, 24, 25, 30}. What is the probability that a temperature of 22 will occur, P(T₂₂)? Select one:

• 1/6
• 1/3
• 1/2
• 6/2

Question 16: Which of the following is an example of a recursive formula? Select one:

• f(x) = 2x
• f(y) = (2y) – 1
• f(n) = f(n-1) + 1
• P (A ∪ B) = P(A) + P(B), where A and B are disjoint and P is the probability function

Question 17: Given: f(x) = (5 * f(x-2)) − 3 ∀ x, f (2) = -3. What is the value of f (15)? Select one:

• 35,156
• -58,593
• -292,968
• 15 is not a member of the described sequence

Question 18: The structural integrity (s) of a building is known to decline by 0.2% per year. If s_{t, t ≥ 0} is the structural integrity of the building at t years after construction, write a recursive relation that is specific for s. Select one:

• st = f(st-1)
• st = 0.002 * st-1
• st = 0.99998 * st-1
• st = st-1 – 0.99998

Question 19: Which of the following is a graph composed of? Select one:

• Edges and links
• Vertices and edges
• Vertices and nodes
• Directional notations

Question 20: Which of the following best describes a Hamiltonian graph? Select one:

• Any graph that contains a circuit
• A graph with a path whose vertex list contains every vertex of the graph
• A graph that contains a circuit, touching each edge of the circuit exactly once
• A graph with a path whose vertex list contains each vertex of the graph exactly once

Question 21: Which of the following graphs is undirected? Select one:

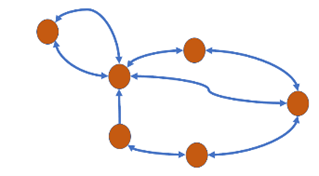
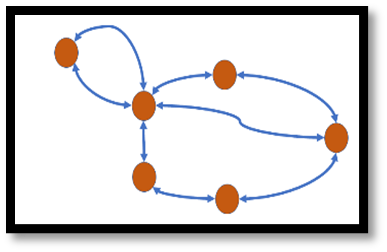
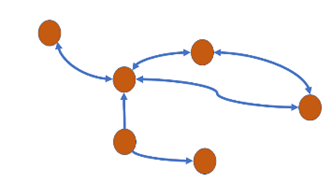
Question 22: In this weighted directional graph, the weights give sensor values that cause the described system to go from one state to another.

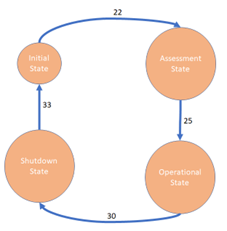
The sensor delivers these values:

Time	Sensor Value
0	0
1	2
2	20
3	25
4	26
5	27
6	30
7	31
8	31
9	32
10	33

What state is the system in after Time₁₀?

Select one:

• Assessment State
• Initial State
• Operational State
• Shutdown State

Question 23: Which of the following would be a way to illustrate a directed graph with this description?

Vertex List	Edge List
V1	{v1, v2}
V2	{v2, v1}
V3	{v2, v3}
V4	{v3, v4}
	{v4, v3}
	{v4, v1}

Select one:

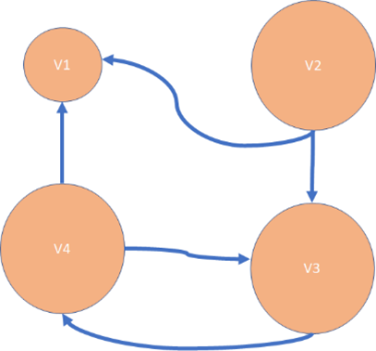
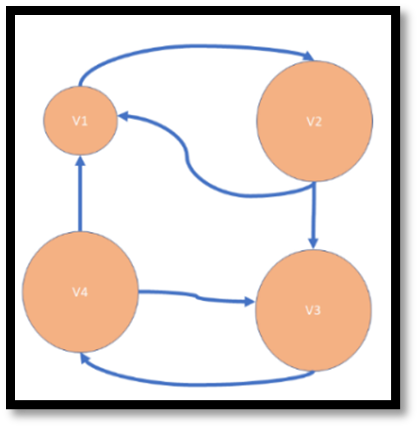
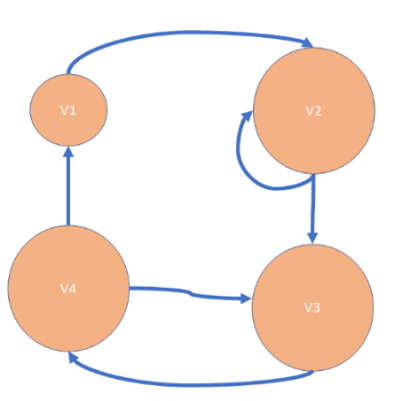
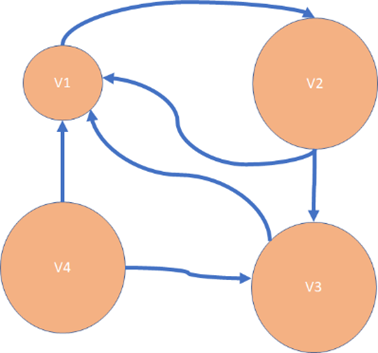
Question 24: Which of the following graphs is a tree? Select one:

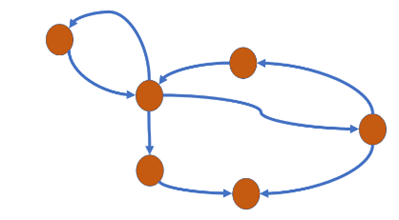
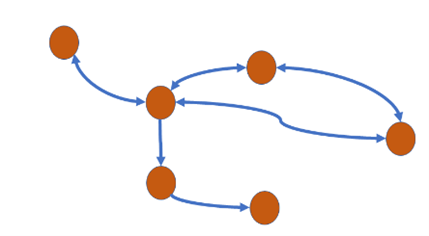
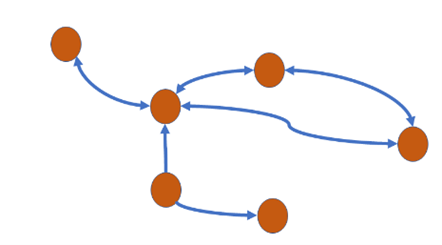
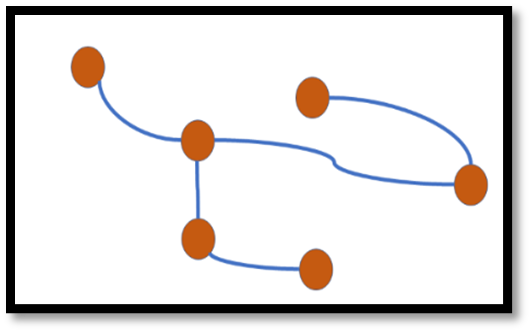
Question 25: Which of the following characteristics describes a binary tree? Select one:

• There are only two cycles
• There are only two subtrees
• Each vertex has one or more subtrees
• Each vertex has no more than two subtrees

Question 26: Which of the following descriptions would be a good explanation of what the system in this image does?

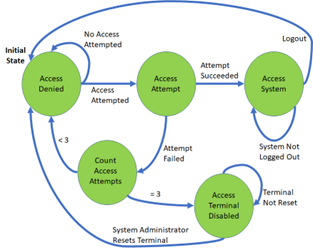
Select one:

• A system terminal is active. It remains active until logout. Upon successful login, the system is accessible until logout.
• A system terminal sits idle. It remains idle until login is attempted. Two failed login attempts are allowed. The third causes the terminal to become disabled. Reset by a system administrator is then required for the terminal to be re-enabled. Upon successful login, the system is accessible until logout.
• A system terminal sits idle. It remains idle until login is attempted. Two failed login attempts are allowed. The third causes the terminal to become disabled. Automatic reset then occurs after five minutes so that the terminal is re-enabled. Upon successful login, the system is accessible until logout.
• A system administrator enables an access terminal. The terminal then sits idle until login is attempted. Two failed login attempts are allowed. The third causes the terminal to become disabled. Reset by a system administrator is then required for the terminal to be re-enabled. Upon successful login, the system is accessible until logout.

Question 27: Which of the following are the essential rules for constructing state diagrams for a system that can only be in one state at a time? Select one:

• There can be multiple transitions specified for a given state data input or external action impacting the state; and for every data input or external action impacting a state, a transition specification must exist
• There can be only one transition specified for a given state data input or external action impacting the state; and for every data input or external action impacting a state, a transition specification must exist
• There can be multiple transitions specified for a given state data input or external action impacting the state; and for every data input or external action impacting a state, a transition specification need not exist since the system is assumed to remain in its present state until a transition event occurs
• There can be only one transition specified for a given state data input or external action impacting the state; and for every data input or external action impacting a state, a transition specification need not exist since the system is assumed to remain in its present state until a transition event occurs

Question 28: What is the maximum size of a set? Select one:

• Finite
• Infinite
• A countable number of elements
• Not countable, but also not infinite

Question 29: Which of the following is this statement an example of?

If x in A implies x in B and x ∉ B, then x ∉ A. Select one:

• Resolution
• Modus Tollens
• Modus Ponens
• Conjunctive specialization

Question 30: Imagine there exists a network of ten computers. These computers can work independently on specific tasks. Tasks are assigned to them by another computer on that same network. There are many ways such a network can be employed. The case at issue involves cameras that capture visual events and transmit the resulting pictures to a receiving computer. That computer assigns pictures to other networked computers for analysis. The analysis of one picture has nothing to do with the analysis of any other picture. If 100 pictures are suddenly sent by the cameras, in how many ways can these pictures be assigned to the analysis computers? Select one:

• 10101010
• 1010010100
• 1001010010
• 100!90!

Question 31: Consider this truth table. What does it tell us?

p�	q�	p∧q�∧�
0	0	0
0	1	0
1	0	0
1	1	1

Select one:

• If any fact is true then the conclusion is true
• The conclusion is true only when all facts are true
• A conclusion can be chosen at random regardless of the facts
• The conclusion is true when all facts are true or when no facts are true

Question 32: Consider the logical equation X = (A ^ ¬B) ∨ (C ^ D). What is the result if A, B, C, D are all true? Select one:

• True
• False
• The result is logically incongruent
• Sheffer Stroke of (A ∪ B) and (C ∪ D)

Question 33: How might we calculate the probability of an event? Select one:

• Set it equal to the probability of the just-prior causal event
• Divide the probabilities of the string of causal events into each other
• Add the probabilities of the individual outcomes that lead up to the event
• Multiply the probabilities of the individual outcomes that lead up to the event

Question 34: What is the mathematical definition of an independent event? Select one:

• P(A∩B) = P(A) ⋅ P(B)
• P(A∩B) = P(A) + P(B)
• P(A∩B) = P(A) / P(B)
• P(A∩B) = P(A) – P(B)

Question 35: What is the difference between a directed graph and an undirected graph? Select one:

• An undirected graph can be traversed in exactly one direction
• A directed graph can be traversed in any direction from any node
• An undirected graph can be traversed in any direction from any node
• A directed graph has only one circuit with a traversal path is specified by directional notation

Question 36: Two separate state machines exist, M1 and M2. M2 takes input from M1. However, M1 operates independently from M2. If M1 has a number of states equal to S1 and M2 has a number of states equal to S2, how many possible state combinations could be achieved? Select one:

• S12
• S22
• S1 + S2
• S2 * S1

Question 37: Consider the set W, X, Y, Z in this figure. What operation on sets W, X, Y gives us set Z?

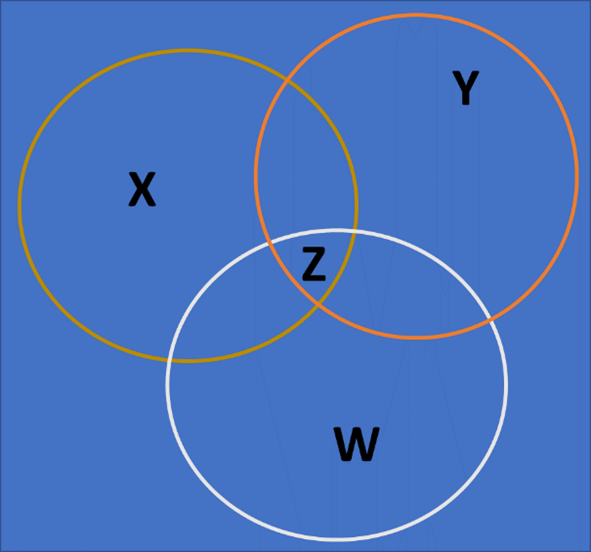
Select one:

• Union of W, X, Y
• Intersection of W, X, Y
• W, X, Y are subtracted from each other
• W, X, Y are subtracted from the universal set

Question 38: Which of the following can be said about all possible outcomes of a random experiment? Select one:

• They cannot be stated, and what will happen cannot be predicted
• They can be stated, and the probability of all possible outcomes lies along a uniform distribution
• They can be stated, but the actual outcome on any given trial cannot be predicted with any certainty
• They can be stated, and the actual outcome on any given trial can be predicted within a specified probability

Question 39: An eCommerce company pays a popular website to display an advertisement for a specific product. Of the 100 customers visiting the product’s website during the ad campaign, only 60 had seen the advertisement. Of the 40 customers purchasing the product, 30 had seen the ad. What is the probability that a visiting customer saw the ad and purchased the product? Select one:

• 25%
• 30%
• 50%
• 60%

Question 40: Why would any application want so many paths between nodes?

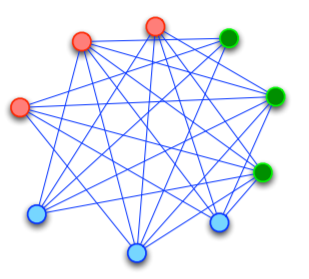
Select one:

• A fully-connected graph is necessary for traversal
• The design consumes appears sophisticated and is likely to be accepted
• Physical traversal requires multiple paths should a given path fail or be bottlenecked
• Application owners can charge for the additional computer time needed to determine the shortest path

Question 41: Which of the following is a binary tree? Select one:

Question 42: Consider sets X and Y in this figure, and assume those are the only sets under consideration. Which of the following equations leaves only the green part of set X?

Select one:

• X = Ø
• Y ↔️ X
• Y ⟶ X
• X = ⇁Y

Question 43: Which of the following is this statement an example of?

Given x in A ∩ B, it follows that x in A. Select one:

• Resolution
• Specialization
• Generalization
• Modus Ponens

Question 44: If there are A elements in set X and we wish to group them in sets having (A−b) non-repeating elements, what formula do we use? Assume that X has no repeating elements. Select one:

• AA−b
• (A−b)!
• P (A, A−b)
• (A/A−b)

Question 45: 3c.2. Assume that a system has three events (E1, E2, E3). One of these must take place before a fourth event, E4, can occur. Which of the following logical equations ensures one of the first three events take place before the fourth event?

Select one:

• E4 = E1 ^ E2 ^ E3
• E4 = E1 v E2 v E3
• E4 ⊕ E1 ⊕ E2 ⊕ E3
• E4 = ᆨE1 v ᆨE2 v ᆨE3

Question 46: What is the negation of this equation?

 ¬ (A ^ B ∨ ¬C ∨ ¬D) Select one:

• ¬A ∨ ¬B ^ C ^ D
• ¬A ^ ¬B ∨ C ∨ D
• A ^ B ∨ ¬C ∨ ¬D
• ¬A ^ ¬B ∨ ¬C ∨ ¬D

Question 47: If P(x) is True for x in C, Q(x) is True for x in D, and P(x) => Q(x), then which of the following is accurate? Select one:

• C is a subset of D
• D is a subset of C
• For some x in D, P(x)
• There exists an x in D

Question 48: If it is true that (a → b → c → … → z), which of the following might be a simple way to state an obvious conclusion? Select one:

• a → z
• a ⇔ z
• a ⇒ z
• a ⇏ z

Question 49: If we wish to prove that (q0 → q1, q1 → q2, …, qn−1 → qn, qn → qn+1, q0 ⇒ qn+1) is true, what type of reasoning could we employ? Select one:

• Analogy
• Deductive
• Inductive
• Reductive

Question 50: In the entertainment industry, customers generally enjoy variety. A producer has a choice between five acts. Three of the acts are aerial and two are magical. Each type of act has one all-female group. If a show is to feature a female act chosen at random, what is the chance that the act will be magical? Select one:

• 20%
• 40%
• 50%
• 60%

Question 51: 6b.2. If the Fibonacci Sequence is defined as Fk = Fk−2 + Fk−1 for k ≥ 2, is this a complete specification? Why? Select one:

• No; you must also know the value of Fk for k = 0
• No; you must also know the value of Fk for k = 1 and k = 2
• Yes; the recursive sequence resolves itself as it proceeds
• Yes; you know everything you need to perform the calculation

Question 52: If an integer n is in N, the set of natural numbers, how would we specify the Kth previous number in the set regardless of the value of n? Select one:

• n + K, n ≥ 0
• n + 1, n ≥ 0
• n – K, n ≥ 0
• n – k, n ≥ K

Question 53: Assume we have a mathematical model composed of Gaussian equations (G) centered at different points along a line. The purpose of the model is to predict the value of the next sample as data streams through the model {D1, D2, D3, …}. The prediction of the value of the next data sample is based on the error of the previous prediction and the value of the now-current data sample. What would be a broad and recursive expression for the prediction component of this model? Error is referred to as E, Data as D, and Predicted Value as P. Select one:

• P = E*G(D)
• Pt = Et*G(Dt)
• Pt+1 = Et-1*G(Dt)
• Pt+1 = Et-1*G(Dt-1)

Question 54: What is the difference between a graph and a tree? Select one:

• A tree has no circular paths
• A tree cannot be fully traversed
• A tree enables direct access to all nodes
• A tree has only one subgraph that contains a cycle

Question 55: Which of the following is correct, using true/false logic? Select one:

• 1 + 1 = 0
• 1 + 1 = 1
• 1 + 1 = 2
• 1 + 1 = 10

Question 56: Which of the following is this statement an example of?

Given x > 1, it follows that x > 0.

Select one:

• Conjunctive specialization
• Disjunctive specialization
• Elimination
• Resolution

Question 57: How do simple induction and strong induction differ? Select one:

• They have different base cases
• They have different inductive steps
• They require different levels of proof
• They have different inductive assumptions

Question 58: A recursive mathematical function is a mathematical function f(a, b, …) that has which of the following properties? Select one:

• Uses far less memory than its explicit version
• Can be calculated once the values of (a, b, c…) are known
• Defines none of its input parameter values (a, b, …) in terms related to those same parameter values
• Defines some or all of its input parameter values (a, b, …) in terms related to those same parameter values

Question 59: Which of the following best describes a spanning tree? Select one:

• A tree within a connected graph that connects all nodes of the graph
• A subgraph of a connected graph that is a tree connecting all nodes of the graph
• A subgraph of a connected graph that connects all nodes of the graph with a minimum number of edges
• A subgraph of a connected graph that is a tree connecting all nodes of the graph with a minimum number of edges

Question 60: Which of the following is this statement an example of?

Given x in A ∪ B’ and x in C ∪ B, it follows that x in A ∪ C.

Select one:

• Resolution
• Elimination
• Disjunctive specialization
• Conjunctive specialization

Question 61: If every vertex of a graph has a distance ≤ 4 from a given vertex v, what is the diameter of the graph? Select one:

• 4
• 8
• ≥ 4
• ≥ 8

Question 62: An Eulerian graph is a graph that does which of the following? Select one:

• Contains a circuit that touches every edge of the graph exactly once
• Contains one or more circuits that touching each edge of the circuit exactly once
• Contains a circuit that contains most edges of the graph, touching each only once
• Has no circuits, and the graph can be traversed by touching every vertex exactly once

Question 63: What are the basic components of a tree? Select one:

• Vertices, edges, edges with or without direction
• Nodes, links, edges without direction, no cycles
• Nodes, links, edges with or without direction, no cycles
• Nodes, links, edges with direction, only one cyclic subtree

Question 64: Which of the following statements about trees and graphs is true? Select one:

• A graph is a tree
• A tree is a graph
• A graph is directed
• A tree can have a loop

Question 65: A special notation shows directional connections between graph vertices and the sensor data required to move from one vertex (system state) to another. For instance, {V1, V2, S} shows the sensor data value required to move from vertex V1 to vertex V2. Which of the following descriptions indicates a system that can be in exactly one of a finite number of states at any given time?

Select one:

Origin State	Target State	Sensor Data Value
V1	V2	10
V2	V4	30
V2	V3	30
V3	V4	40
V4	V3	20
V4	V1	30

Origin State	Target State	Sensor Data Value
V1	V2	10
V2	V1	50
V2	V6	30
V6	V3	40
V3	V2	30
V2	V4	30
V4	V5	30
V5	V6	50

Origin State	Target State	Sensor Data Value
V1	V2	10
V2	V1	50
V2	V6	30
V6	V3	40
V3	V2	30
V2	V4	30
V4	V5	30
V5	V6	50

Origin State	Target State	Sensor Data Value
V1	V2	10
V2	V1	50
V2	V6	30
V6	V3	40
V3	V2	30
V2	V4	20
V4	V5	30
V5	V6	50

Question 66: Consider this situation: The main valve is closed when time equals six and the computer is waiting for another instruction, or when the computer is first initialized. What is the valve’s state when time equals five and the computer is waiting for another instruction, and the computer is ten seconds past its initialization phase? Select one:

• The valve is closed
• The valve is not closed
• The valve remains in its present state
• The valve will alternate between open and closed

Question 67: How could the series for 12, 22, 32, …, n2, … and k0, k1, k2, …, kn, …, be solved when k is a constant? Select one:

• By deduction on n for both series
• By induction on n for the first series and induction on k for the second series
• By induction on n2 for the first series and induction on kn for the second series
• By induction on n for the first series and induction on both k and n for the second series

Question 68: Conditional probability is given symbolically as P(A|B). Which of the following is the expansion of this rule? Select one:

• P(A)/P(B)
• P(A∪B)/P(B)
• P(A∩B)/P(A)
• P(A∩B)/P(B)

Question 69: A random number generator draws integers from a uniform distribution defined on the range 1…100. A seed is selected and then two sets of numbers are sequentially generated: S1 = {2, 16}, S2 = {37, 99, 41, 2}. Considering these two sets only, what can be said about S1 and S2? Select one:

• S1 and S2 are independent
• S1 and S2 are not independent
• S1 and S2 were generated using a weak seed
• S1 and S2 were generated using a strong seed

Question 70: The binomial coefficient (nk) is how we write “the number of groups attained if n objects are partitioned into unique groups having k unique members”. If we specify the recursive version of the calculation as (nk)=(n−1k) +(n−1k−1) if n>k>0, what is missing in the specification? Select one:

• The result when n=0
• The result when k=0
• The result when k<0
• The result when n=0 and k=0

Introduction to Discrete Structures

Discrete structures are fundamental concepts in mathematics and computer science that deal with countable, distinct, and separate entities. They are central to the study of algorithms, data structures, and various other aspects of computing and discrete mathematics. Here are some key topics within discrete structures:

1. Set Theory: The study of sets, which are collections of distinct objects. Key concepts include set operations (union, intersection, difference), subsets, power sets, and Cartesian products.
2. Logic: The study of formal reasoning. It involves propositional logic (dealing with statements that are either true or false) and predicate logic (which deals with predicates and quantifiers). Topics include logical operators, truth tables, logical equivalence, and inference rules.
3. Functions and Relations: Functions are mappings from one set to another, while relations are generalizations of functions that associate elements of one set with elements of another (or the same) set. Concepts include domain, range, injectivity, surjectivity, bijectivity, and composition of functions.
4. Combinatorics: The study of counting, arrangement, and combination of discrete structures. It includes topics like permutations, combinations, the pigeonhole principle, and binomial coefficients.
5. Graph Theory: The study of graphs, which are mathematical structures used to model pairwise relations between objects. Topics include vertices, edges, paths, cycles, connectivity, and graph coloring.
6. Trees: A type of graph with no cycles, commonly used in data structures. Key concepts include binary trees, tree traversal methods, and applications in hierarchical data representation.
7. Algorithms: The study of step-by-step procedures for performing computations. Important aspects include sorting and searching algorithms, algorithm complexity (time and space), and algorithm design paradigms (such as divide and conquer, dynamic programming, and greedy algorithms).
8. Number Theory: The study of properties of integers. Important topics include divisibility, primes, congruences, and modular arithmetic.
9. Boolean Algebra: The study of algebraic structures that capture the essence of logical operations. It involves binary variables and operations such as AND, OR, NOT, and their properties.
10. Formal Languages and Automata: The study of abstract machines and languages. Topics include finite automata, regular expressions, context-free grammars, and Turing machines.

These topics are foundational for understanding and solving problems in computer science and discrete mathematics. Each area offers a rich set of concepts and techniques that are widely used in theoretical and practical applications.